「1」插入排序
void insertSort(int arr[],int length){
for (int i = 1; i < length; ++i) {//初始默认单个元素a[0]作为有序序列,以a[1]作为待插入元素
if (arr[i-1]>arr[i]){//如果待插入元素的前一个数(有序序列的最后一个数)比待插入元素大则开始进入循环,(反之如果前一个数比待插入元素小或等于,则有序序列中所有的元素都比它小或等于)
int j = i-1;
int temp = arr[i];//移动中可能会覆盖,需要备份
while (j>=0 && arr[j] > temp){//前面没有要比较的元素了也退出循环,将待插入元素依次与有序序列中的元素比较,如果比它大则向后移(反之如果比待插入元素小或等于,则这个元素及这个元素以前的元素都比它小或等于)
arr[j+1] = arr[j];
j--;
}
arr[j+1] = temp;//插入到前面的元素都比它小或等于,后面的元素都比它大的位置
}
}
}「1.2」二分查找插入排序
//由于查找序列默认有序,查找插入点时采用二分查找
void binarySearchInsertSort(int arr[],int length){
for (int i = 1; i < length; ++i) {
if (arr[i-1]>arr[i]){
int low = 0;
int high = i-1;
int mid = (low + high) / 2;
int temp = arr[i];//移动中可能会覆盖,需要备份
while (low <= high)
{
if (temp < arr[mid])high = mid - 1;
else low = mid + 1;
//如果查找到temp=arr[mid],找到相同元素,则low移到它的右边,最终low=high=mid归结到一点时会在有序序列中相同元素的右边,此时该归结点一定大于temp,high=mid-1,插入时按high+1插入即在它的右边
//(插入排序是用后面的元素与前面的有序序列对比,所以为保证稳定性找到相同元素的插入点后应插入到它的右边)
//如果到了low=high=mid,temp<此时位置的元素,high=mid-1,low>high退出循环,high+1即为插入点,high+1及到temp已存在的元素会预先后移
//无论如何最终都会归结到low=high=mid,temp比它大则low=mid+1,high+1(mid的右边)为存放点,temp比它小则high=mid-1,high+1(mid自己及到temp会预先后移,mid为存放点)
mid = (low + high) / 2;
}
for (int j = i-1; j >= high+1; j--) {//temp以前的元素一直到插入点本身的元素右移
arr[j+1] = arr[j];//集体右移为temp腾空间
}
arr[high+1] = temp;
}
}
}「2」希儿排序
“拜托了另一个我”
//以gap为步长进行插入排序,先追求部分有序再追求整体有序(此排序为不稳定排序:对于没有被划分到一组的相同元素,可能在不同组的排序时他们的相对位置会发生改变)
void ShellSort(int arr[],int length){
int gap = length / 2;
while (gap>0){//每轮对以gap为增量的元素划分为一组,要确保最后一轮gap一定为1
for (int i = gap; i < length; i++) {//对该轮gap下的每组进行排序,组内插排时移动比较的增量统一为gap,注意由于是i++所以组与组之间是交替进行的
if (arr[i-gap]>arr[i]){
int j = i-gap;
int temp = arr[i];
while (j>=0 && arr[j] > temp){
arr[j+gap] = arr[j];
j-=gap;
}
arr[j+gap] = temp;
}
}
gap = gap / 2;
}
}「3」冒泡排序
void swap(int &value1, int &value2) {
int temp;
temp = value1;
value1 = value2;
value2 = temp;
}
void BubbleSort(int arr[], int length){
//“冒上岸”:意思是冒泡排序每轮冒上岸的元素的位置为其最终位置,认定为有序
//最后一个要进行冒泡的元素一定为最大的(假设冒泡排序为降序),所以无需执行冒泡,i<length-1即实际范围0-length-2
for (int i = 0; i < length-1; ++i) {//初始状态无一个元素"冒上岸",第一轮两两比较需一直比较到arr[0]
bool flag = false;//设置本轮是否发生过交换的标记位
for (int j = length-1; j > i; --j) {//从最后一个元素两两比较到已“冒上岸”的元素(不包括"冒上岸"的)
if (arr[j-1]>arr[j]){
swap(arr[j-1],arr[j]);
flag = true;//存在逆序发生交换
}
}
if (flag == false)return;//如果除"冒上岸"元素以外,其余所有元素已经两两有序(比较时全都没有进行过交换),则表示整个表已经有序,程序结束
}
}「4」快速排序

//就算high前移时(pivot后)有和pivot相等的元素不会填到它前面,low和high指针相汇点(pivot的最终位置)还是可能填在这个相等元素的后面,所以是不稳定排序
int Partition(int needPartArray[], int low, int high) {
int pivot = needPartArray[low];//将最头元素作为pivot,(”挖空”)
while (low < high) {//如果partition传入只有一个元素的待排序列时,就会出现low大于high(上一次的划分点为这个元素自己high=上一次的划分点-1),low大于等于high则本次划分完毕
while (needPartArray[high] >= pivot && low < high)high--;//找比pivot小的,且low始终在high左边
needPartArray[low] = needPartArray[high];//放在pivot左边("填空"),low等于high时相当于不做任何操作
while (needPartArray[low] <= pivot && low < high)low++;//找比pivot大的,且low始终在high左边
needPartArray[high] = needPartArray[low];//放在pivot右边(”填空“),low等于high时相当于不做任何操作
//最后这个low++后也有可能low等于high此情形交给此partition中第一层while(low < high)判断
}
needPartArray[low] = pivot;
//填补low等于high(pivot的最终位置),low大于high表示只有一个元素,上一次划分点low仍为本次划分点
return low;
//返回本此划分点
}
void QuickSort(int arr[], int low, int high) {
if (low < high) {//当low>=high时递归结束(只有一个元素时)
int pivot = Partition(arr, low, high);//求划分点
QuickSort(arr, pivot + 1, high);//对划分点的右侧再划分
QuickSort(arr, low, pivot - 1);//对划分点的左侧再划分
//注意右边处理到最深层后,接着退到上一次递归,处理左边时,low和high值为上一次递归传入的low和high(对应的二叉树的左树)
}
}「5」简单选择排序

void swap(int &value1,int &value2){
int temp;
temp = value1;
value1 = value2;
value2 = temp;
}
//每次从无序序列中选一个最小的加入有序序列
//不稳定排序比如2 2 1,
//冒泡排序是仅限相邻的两两比较两两交换(相对位置不变,是稳定排序)
//选择排序是开头一个元素与剩余整个序列每个比较找最小的后再直接换到了最前面(不稳定排序)
void SelectSort(int arr[],int length){
for (int i = 0; i < length-1; ++i) {
int min = arr[i];
for (int j = i+1; j < length; ++j) {
if (arr[j]<min)swap(arr[j],min);
}
arr[i] = min;
}
}「6」堆排序

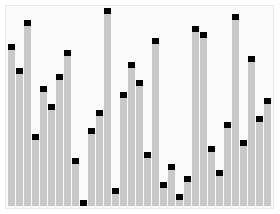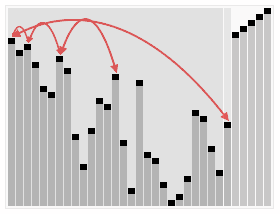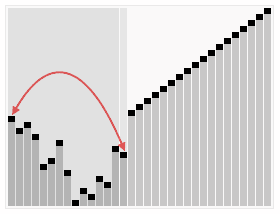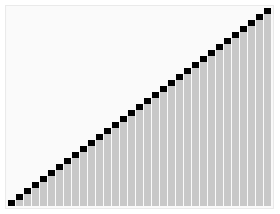
//堆排序为不稳定排序,属于选择排序,其找最大的过程通过构建堆完成
void swap(int &val1, int &val2) {
int temp;
temp = val1;
val1 = val2;
val2 = temp;
}
void AdjustHeap(int arr[], int key, int MaxNo) {
for (int j = 2 * key;
j <= MaxNo; j *= 2) {//增量可更新到该分支的左孩子,结点有左孩子一定小于等于MaxNo,逐层左右孩子与根比较逐层调整为大根堆,待调整的分支结点最深只会下降到MaxNo以内
//判断最后一个分支结点是否有右孩子(由完全二叉树的性质其它分支结点一定有左右孩子且编号一定小于MaxNo)
//分支结点有右孩子(完全二叉树的分支结点要么只有左孩子且该节点为最后一个结点,要么左右孩子都有)
if (j < MaxNo && arr[j + 1] > arr[j])j++;//选出左右孩子中大的一个
if (arr[key] > arr[j])break;//比孩子都大,无需调整
else {
swap(arr[key], arr[j]);//将大的放到根部
key = j;//原key下降到了j,继续切换到交换点j继续向下调整
}
}
}
void BuildMaxHeap(int arr[], int maxNo) {
//为保证完全二叉树性质,数组有效数据默认从1开始,
// MaxNo为最后一个元素编号,最后一个元素的父结点即⌊maxNo/2⌋
for (int i = maxNo / 2; i > 0; --i) {//所有的分支结点都需要构成大根堆
AdjustHeap(arr, i, maxNo);
}
}
void HeapSort(int arr[], int maxNo) {
BuildMaxHeap(arr, maxNo);//构建大根堆
for (int i = maxNo; i > 1; --i) {
//将大根堆的首个元素加入到数组末尾(为其最终位置),然后调整剩余元素为大根堆,继续加入首个元素到末尾,直到只剩最后一个有效元素时无需调整
swap(arr[1], arr[i]);
AdjustHeap(arr, 1, i - 1);
}
}
「7」归并排序
图文来源(感觉描述的挺清楚的):https://www.runoob.com/w3cnote/merge-sort.html
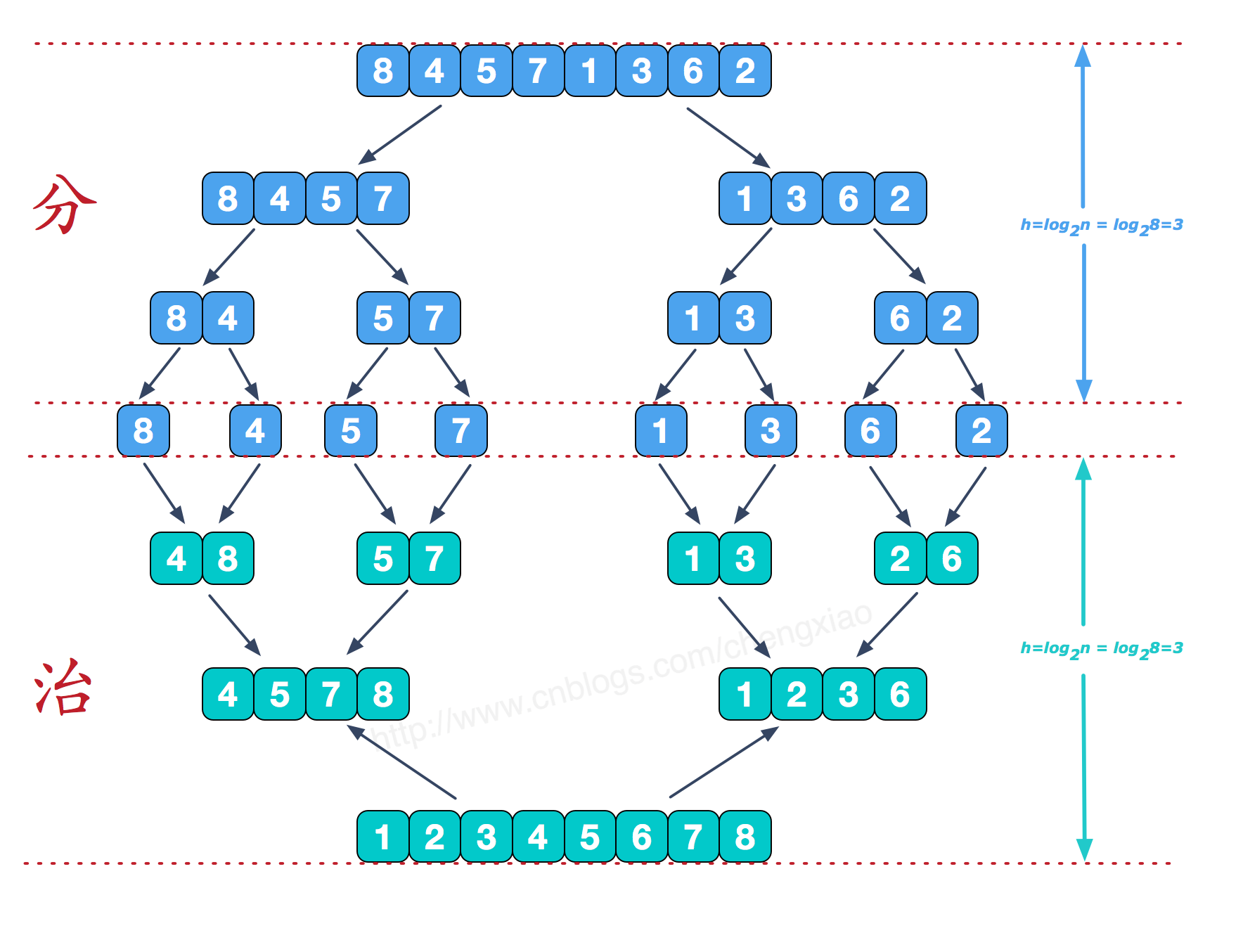
分阶段可以理解为就是递归拆分子序列构造二叉树的过程,递归深度为log2n。空间复杂度=O(n)(递归深度log2n+辅助空间大小n),时间复杂度=O(nlog2n)(每层平均比较n次,共log2n层)
治阶段,合并相邻有序子序列,如上图的最后一次合并,将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],步骤如下图:
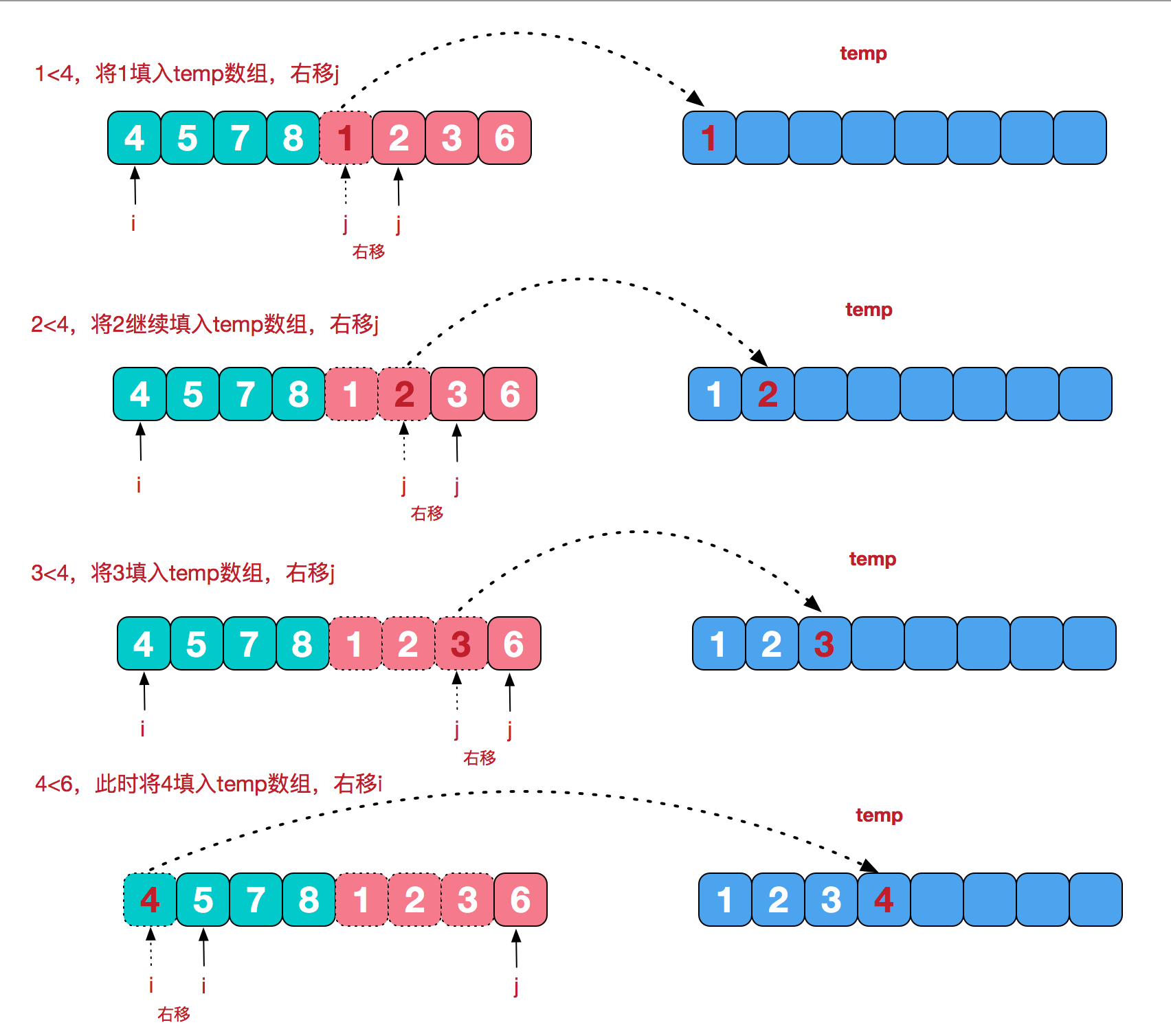
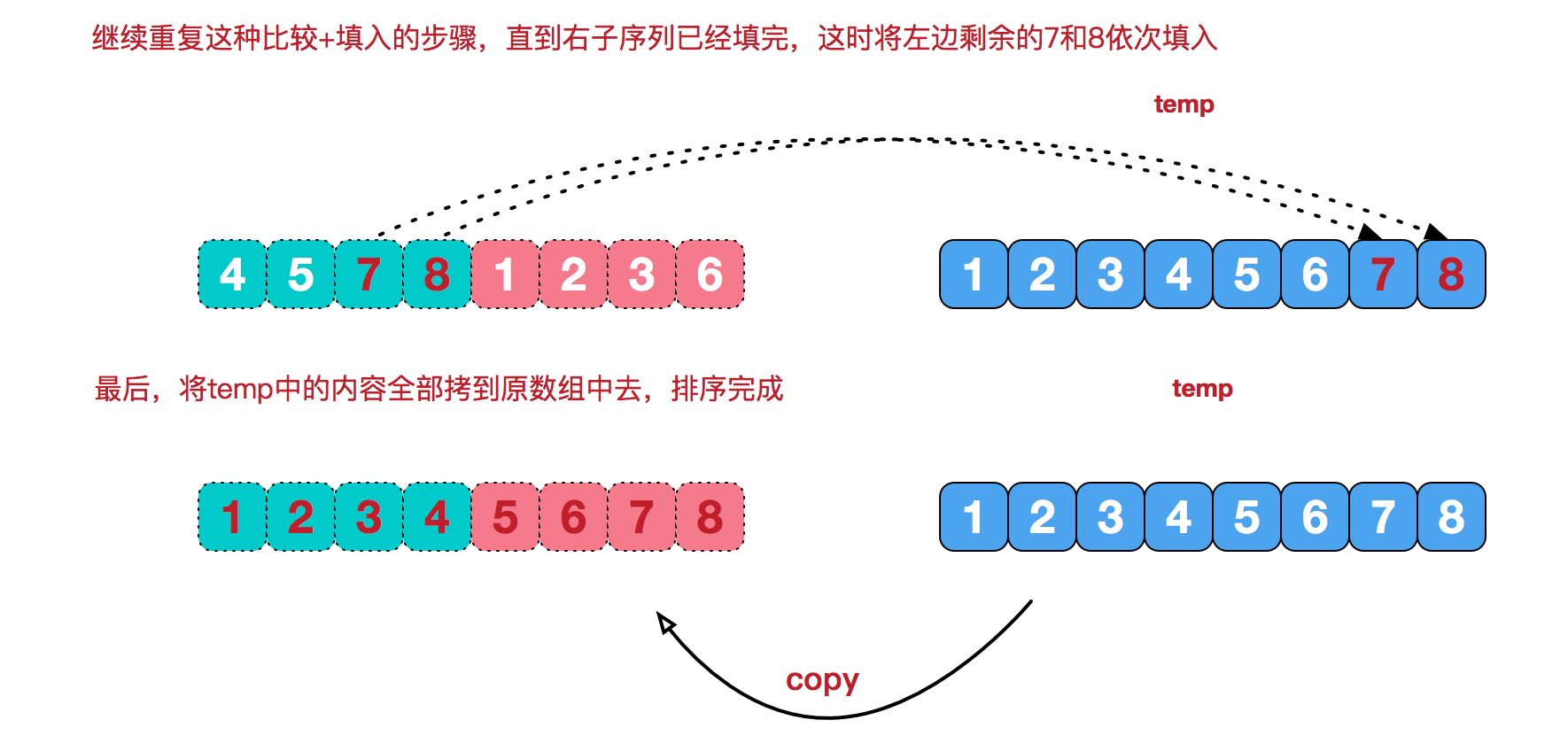
//稳定排序
//辅助数组,长度与待排序数组相同
int *auxArr = (int *)malloc(sizeof(int)*N);
//执行二路归并(待归并的两组数组得分别有序low~mid一组,mid+1~high一组)
void merge(int arr[],int low,int mid,int high){
for (int i = low; i <= high; ++i) {
auxArr[i] = arr[i];//复制数组元素到辅助数组对应位置
}
int i;
int j;
int k;
for (i = low,j = mid + 1,k = i; i <=mid&&j<=high ; ++k) {
//i:第一组有序数组下标,j:第二组有序数组下标,k:在原数组中的存放位置
//在两组有序数组的当前开头元素中选较小的或选第一组的相同当前开头元素优先放入原数组相应位置
if (auxArr[i]<=auxArr[j])arr[k] = auxArr[i++];//等号用于确保稳定
//再将i(第一组有序数组下标)增1,原数组下标位置增1
else
arr[k] = auxArr[j++];
//否则将j(第二组有序数组下标)增1,原数组下标位置增1
//直到有一组数组执行到了组内末尾(i>mid或j>high),已率先将所有元素存入到了原数组中,则另外一个有序数组中的剩余元素一定是最大的几个
}
//检测哪一组还有剩余元素
while (i<=mid)arr[k++] = auxArr[i++];//先arr[k] = auxArr[i],再k++,i++
while (j<=high)arr[k++] = auxArr[j++];
//将还有剩余元素的数组迁移到元素组
}
//逐步划分,递归构造一颗倒立的二叉树,先由两片叶子结点组成的两组归并,再到往下逐层递归的向根归并(先归并好根的左子树)
void MergeSort(int arr[],int low,int high){
if (low<high){
int mid = (low + high) / 2;
MergeSort(arr,low,mid);
MergeSort(arr,mid+1,high);
merge(arr,low,mid,high);//先划分再归并
}
}




Comments NOTHING